Idee
Bei der geometrischen Verteilung liegt folgender Gedanke zugrunde: Wir haben ein Bernoulli-Experiment mit einer Erfolgswahrscheinlichkeit von 
. Nun fragen wir uns, wie oft wir dieses Experiment ausführen müssen, bis der erste Erfolg eintritt.
Das meiner Meinung nach schönste Beispiel zur Veranschaulichung ist das vom betrunkenen Pförtner: Er hat einen Schlüsselbund mit 8 Schlüsseln, und einer davon öffnet das Tor, vor dem er steht. Da er aber betrunken ist, fällt ihm nach jedem Fehlversuch der Schlüsselbund herunter, und er weiß nicht mehr, welchen Schlüssel er schon probiert hat.
Jeder einzelne Versuch ist also ein Bernoulli-Experiment mit der Erfolgswahrscheinlichkeit 
. Da er 8 Schlüssel hat, ist ein zufällig gewählter Schlüssel mit einer Wahrscheinlichkeit von 
der richtige.
Mit der geometrischen Verteilung können wir dieses Experiment nun beschreiben, und die Wahrscheinlichkeiten dafür bestimmen, dass er zum Beispiel genau einen Versuch, genau vier Versuche, oder höchstens fünf Versuche benötigt.
Parameter
Die geometrische Verteilung hat nur einen Parameter, nämlich , die Erfolgswahrscheinlichkeit bei einem einzelnen Versuch. Im Beispiel des betrunkenen Pförtners ist . Benennen wir die Zufallsvariable für das Experiment mit 
, wird die geometrische Verteilung dargestellt durch
in unserem Beispiel
Träger
Es gibt theoretisch keine Obergrenze für die Anzahl der Versuche, die der Pförtner benötigt. Jeder neue Versuch gelingt nur mit einer Wahrscheinlichkeit von 
, daher kann jede natürliche Zahl von 0 bis unendlich annehmen:
Dichte
Die Dichte der geometrischen Verteilung lautet
Diese Dichte kann man sich leicht veranschaulichen: Um die Wahrscheinlichkeit zu bestimmen, dass der Pförtner beim dritten Versuch den richtigen Schlüssel erwischt, also 
, muss er nacheinander zwei Fehlversuche (mit Wahrscheinlichkeit 
und einen Treffer (mit Wahrscheinlichkeit ) machen. Die gesamte Wahrscheinlichkeit ist also das Produkt der drei Bernoulli-Experimente, also 
. Das kann man zu 
zusammenfassen. Setzt man nun allgemein ein 
statt der 2 ein, erhält man die Dichte der geometrischen Verteilung, nämlich das Produkt von 
Mißerfolgen und einem Erfolg.
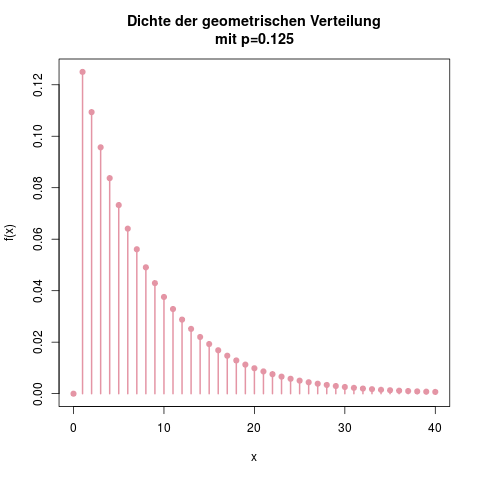
Die Dichte der geometrischen Verteilung für das Beispiel des betrunkenen Pförtners. Die -Achse ist abgeschnitten, da die Dichte nach rechts ins Unendliche weitergeht. Die Wahrscheinlichkeiten für mehr als ca. 30 Versuche werden verschwindend gering, aber sind theoretisch immer noch im Bereich des Möglichen. Man sieht auch, dass 
, die Wahrscheinlichkeit, dass gleich beim ersten Versuch der Treffer erfolgt, genau ist.
Verteilungsfunktion
Die Verteilungsfunktion lässt sich mit Hilfe einer Rechenregel für Wahrscheinlichkeiten herleiten. Wir suchen nämlich gemäß der Definition der Verteilungsfunktion den Wert 
, also die Wahrscheinlichkeit, dass der Pförtner maximal Versuche benötigt, um das Tor zu öffnen. Dieser Wert ist nur über eine Summe der Dichten von 
bis 
zu erhalten. Aber die Gegenwahrscheinlichkeit ist einfach:
Die Wahrscheinlichkeit 
, dass der Pförtner mehr als Versuche benötigt, ist leicht zu berechnen. Es ist nämlich das Produkt von Fehlversuchen, also 
. Und das ist genau das Gegenereignis vom Ereignis "maximal Versuche".
Mit der folgenden Regel erhalten wir dann die Verteilungsfunktion:
Die Verteilungsfunktion der geometrischen Verteilung ist also
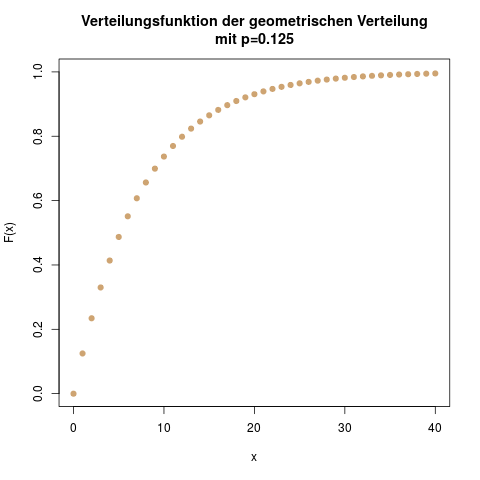
Die Verteilungsfunktion der geometrischen Verteilung. Ihr Wert nähert sich im Unendlichen der 1 an, erreicht ihn aber nie exakt.
Erwartungswert
Der Erwartungswert der geometrischen Verteilung ist
Bei 8 Schlüsseln, also , braucht der Pförtner also im Durchschnitt 8 Versuche, um das Tor zu öffnen.
Varianz
Die Varianz der geometrischen Verteilung berechnet man durch
Alternative Darstellung
In manchen Büchern bzw. Skripten begegnet man auch einer alternativen Darstellung der geometrischen Verteilung. Hier ist mit nicht wie hier die Anzahl der Versuche bis (inklusive!) zum ersten Treffer gemeint, sondern die Anzahl der Fehlversuche vor dem ersten Treffer. Wenn ich also modellieren will, dass der betrunkene Pförtner drei Fehlversuche macht, bis er im vierten Versuch das Tor öffnet, so berechne ich in der hier besprochenen Darstellung 
, aber in dieser alternativen Darstellung wäre es stattdessen 
. Die Formeln für Dichte, Verteilungsfunktion, und Erwartungswert verändern sich natürlich entsprechend, so dass dieselben Wahrscheinlichkeiten herauskommen.
Klausuraufgabe
Zu Beginn eines Mensch-ärgere-dich-nicht-Spiels muss man so lange würfeln, bis man eine 6 erhält, erst dann kann man das Spiel starten. Wenn man an der Reihe ist, darf man maximal dreimal würfeln – hat man dann noch keine 6 geworfen, ist der nächste Spieler dran.
Berechne hierfür
a) die Wahrscheinlichkeit, gleich beim ersten Versuch eine 6 zu würfeln.
b) die Wahrscheinlichkeit, beim dritten Versuch eine 6 zu würfeln.
c) die Wahrscheinlichkeit, irgendwann in der ersten Runde (d.h. nach spätestens drei Würfen) eine 6 zu werfen.
d) die Wahrscheinlichkeit, in der ersten Runde (d.h. nach drei Würfen) noch keine 6 erhalten zu haben.
